Mechanistic Modelling in Ecology
Written on 2019-04-22
Few words in science are as imprecise as the term “modelling”. It is a term applied to a whole range of techniques, which often have nothing at all in common. Small wonder, then, that many of my ecologist colleagues don't know what I mean when I say that I am doing “mechanistic modelling”. This is an attempt to clear up that misunderstanding, and to explain where ecological modellers like myself fit into the wider landscape of ecological research.
Patterns and Processes
Ecology is all about exploring patterns and processes. We observe patterns in nature and ask ourselves: “What processes cause these patterns?” Why does this species spread so rapidly in this environment? Why do migrating birds arrive when they do, and why are they doing so earlier than in previous years? What happens to a dead tree, and why is that important for the rest of the forest?
There are rules to how nature works, and we have spent decades and centuries figuring out what these rules are. But nature is a highly complex system: everything interacts with everything else, so in any given situation it can be almost impossible to say what processes are at work in which ways. In other words, linking an observed pattern to a set of processes, or even predicting a future pattern from a set of current processes, is very, very hard. That is what modelling is all about.
A different combination of processes (arrows) can give rise to very different patterns (curves). The aim of mechanistic modelling is to figure out how the two layers are connected.
Analysing Patterns: Statistical Modelling
One approach is to simply ignore the underlying processes and extrapolate the observed patterns to predict what will happen in the future. As a trivial example, if you have a culture of bacteria that replicate every hour, you can predict that in six hours, it will contain 64x as many individuals as it does now. Or you can look at the environmental conditions in which a species occurs at the moment, and use these to predict where else it could potentially live – a method known as Species Distribution Modelling.
This is a valid approach if you need short-term quantitative predictions, but it soon runs into problems. In the bacteria example, the population obviously cannot keep growing forever, because it will soon deplete its resources as it reaches its environment's carrying capacity. Nonetheless, describing real-world data with statistical models (and potentially using these for future predictions) is an important part of ecological research.
Analysing Processes: Mathematical Modelling
Instead of just looking at the patterns, one can also try to express the process one is interested in as a mathematical equation. Many ecological questions are inherently numeric and therefore well suited to mathematical analysis. Population dynamics like reproduction, life-history stages, or predation can quite easily be represented using partial differential equations or other mathematical constructs.
The classic example here is, of course, the Lotka-Volterra equation set:
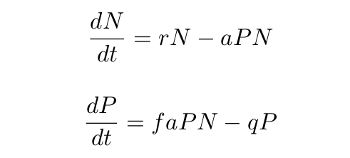
which relates the growth of the prey population size N to that of the predator
population size P. When plotted out, this gives the well-known cyclical species
abundances:
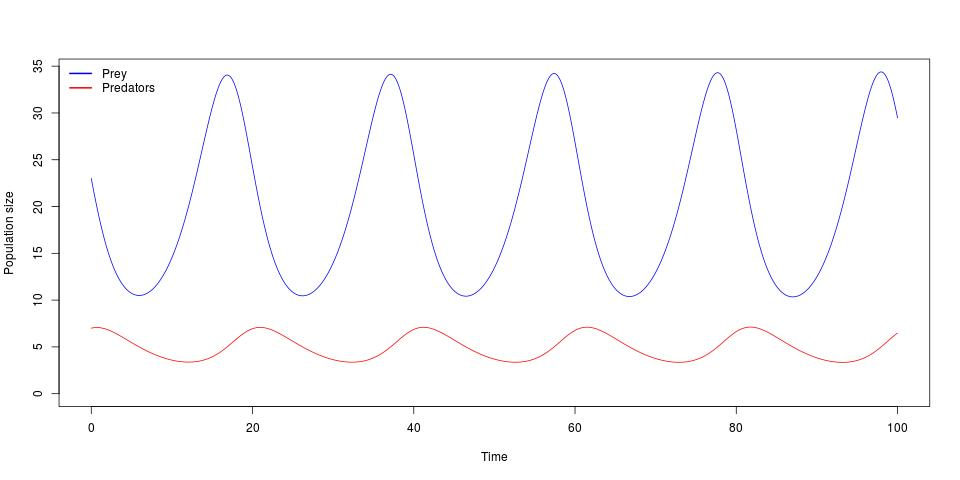
Such models are heavily used in theoretical ecology, as they are relatively easy to work with and allow biological phenomena to be succinctly expressed in the language of mathematics. However, despite their tractability, they also have several important downsides.
First, the amount of complexity that can be modelled with them is limited. Although they are great for investigating individual processes, constructing and analysing mathematical models with multiple processes becomes more and more difficult with every added variable. Soon, they become too unwieldy to be of any practical use. In a field dedicated to studying complex systems, this is not a good property.
Secondly, there are numerous aspects of ecology that are difficult or even impossible to cast into the rigid mould of an equation. The concept of space, or heterogeneity, or behaviour that is conditional upon external or internal cues, are all hard to convey in a formula.
Putting it together: Mechanistic Modelling
Overcoming these challenges, then, brings us to mechanistic modelling. (Confusingly, this is also known by other terms that either mean the same thing or are closely related, such as dynamic modelling, simulation modelling, or agent- or individual-based modelling.)
In mechanistic modelling, we basically build our own ecosystem inside the computer. Crucially, we do not do this at the pattern level, but at the process level. Looking at the system we wish to study, we try to figure out which processes are important for the patterns we are interested in. We then go and implement these processes as computer code in our model, let it run, and see if the processes we chose are sufficient to produce the pattern we wanted to investigate.
The key idea in this is that the patterns our model produces are not coded for explicitly, but emerge from the processes we chose. Therefore, the more real-world patterns our model can reproduce, the greater our confidence that our choice and implementation of processes reflects what is actually going on in nature. Thus, mechanistic modelling bridges the gap between patterns and processes, and helps to explain the mechanisms behind the world we see.
The benefit to this approach is that we can take on much greater complexity. For one, we are not limited to a mathematical notation, but instead have the whole power of modern computer programming languages at our disposal. Instead of having to sum up an entire population in a single numeric variable, we can simulate every single individual in an ecosystem, and its interactions with every other individual. We have total control over every aspect of our virtual world, and are only limited by the computing power we have available. Therefore, we can carry out experiments on a scale that would never be feasible in real life. And we can analyse the outcomes of our experiments in a myriad different ways, because we can find out literally everything that's going on inside our model.
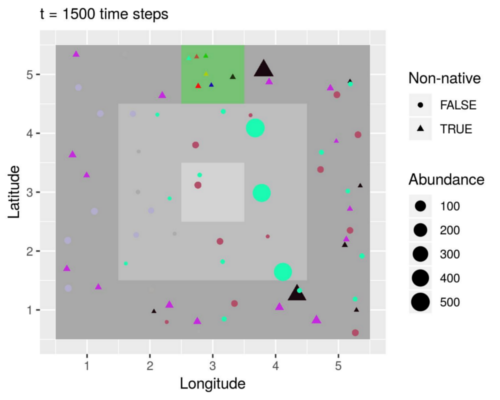
A simulated island inhabited by populations of native (circles) and non-native (triangles) species. Non-natives were introduced in the green patch, but only those that were sufficiently adapted to the local environment managed to spread (black and purple triangles). Species distributions also reflect a radial temperature gradient (grey-scale background) and a longitudinal precipitation gradient. These are all examples of natural patterns produced by the working together of the seven processes implemented in the model. (Vedder, Leidinger & Cabral, in press)
Conclusion
Mechanistic modelling is a powerful tool to study the complexity of the ecosystems that surround us. It allows us insights we could not get by other means and, depending on the application, enables qualitative and/or quantitative predictions to be made.
Of course, there are challenges – dealing with complexity is never easy. Implementing a model is hard and requires a lot of technical expertise. Showing that it adequately reflects real-world conditions is even harder.
But even while one is implementing a model, one is already learning. Mechanistic models build on a broad base of prior knowledge. Due to the wide range of processes they include, one already has to know a lot about the target system before the model is finished. Pulling together all the information needed is an excellent exercise in scientific synthesis.
Like all tools, mechanistic models have their shortcomings. But as I wrote previously:
Simulations can never replace studying the great outdoors. But if they set us thinking, or allow us to experiment more freely than we otherwise could, or show us what might happen, they have fulfilled their purpose.
Further reading
Grimm, V. & Railsback, S.F., 2012. Pattern-oriented modelling: a “multi-scope” for predictive systems ecology. Philosophical Transactions of the Royal Society B, 367, pp.298–310.
DeAngelis, D.L. & Grimm, V., 2014. Individual-based models in ecology after four decades. F1000prime reports, 6:39.
Grimm, V. & Railsback, S.F., 2005. Individual-based Modeling and Ecology, Princeton: Princeton University Press.
Tagged as biology, ecology, favourites
